Крышки люков, спасающие пешеходов от падений в колодцы и мешающие автомобилистам, чаще всего круглые. Выбор такой формы объясняется соображениями безопасности: квадратная крышка при сдвиге может провалиться в люк, поскольку сторона квадрата меньше его диагонали. А у круга есть замечательное свойство — эта фигура постоянной ширины.

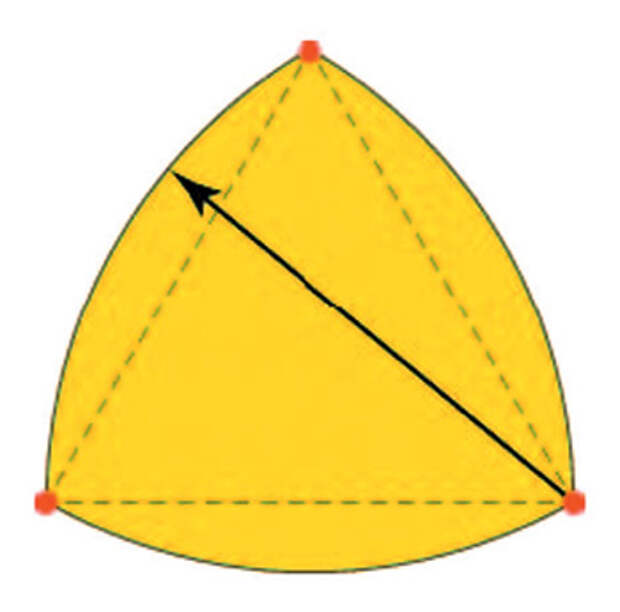
Постоянная ширина означает, что при «обхвате» фигуры двумя параллельными прямыми ширина полосы между ними будет постоянной, независимо от направления прямых.

А есть ли на плоскости помимо круга другие фигуры постоянной ширины? Оказывается, есть, и их много. Самая простая и самая знаменитая — треугольник Рёло. Точнее говоря, эта фигура только напоминает треугольник, её граница — дуги трёх окружностей с центрами в вершинах правильного треугольника, радиусы которых равны длине стороны треугольника. Можно показать (и проверить с помощью штангенциркуля), что при обхвате треугольника Рёло параллельными прямыми точками касания прямых будут одна из его вершин и какая-то точка на противолежащей этой вершине дуге окружности. Так как радиусы всех дуг равны, то результат «измерения» всегда будет одинаков.

По той же схеме, что и для тре-угольника, фигура постоянной ширины строится на любом правильном n-угольнике, имеющем нечётное число вершин. Можно построить и несимметричные фигуры постоянной ширины.

Свойство постоянной ширины легко продемонстрировать. Для этого надо изготовить набор роликов с профилями различных фигур фиксированной постоянной ширины. Если положить ролики на горизонтальную поверхность и накрыть дощечкой, то при качении роликов дощечка будет перемещаться горизонтально.

Все фигуры данной постоянной ширины имеют одинаковый периметр. Есть у таких фигур и своеобразная иерархия: наи-большая площадь у круга, наименьшая — у треугольника Рёло.

Благодаря своим геометрическим свойствам фигуры постоянной ширины находят применение в различных областях.

Первый пример. Вы опускаете монету в автомат, и она отправляется в путь по монетоприёмнику. Чтобы монета не застряла, можно, конечно, расширить трубку металлоприёмника. А можно изготавливать монеты в виде фигур постоянной ширины, тогда они не застрянут в трубке, даже вращаясь. Простейшая фигура постоянной ширины, как мы знаем, — круг, в форме которого делают большинство монет. Но есть и исключения. В Великобритании 20- и 50-пенсовые монеты имеют форму фигуры постоянной ширины, построенной на правильном семиугольнике. Такая же форма у монет достоинством в полдинара, находящихся в обращении в Иордании. Изготовление монет в виде фигур постоянной ширины, отличных от круга, позволяет экономить металл, ведь, как мы знаем, при фиксированной ширине круглая монета — самая металлоёмкая.

Второй пример. До наступления цифровой эпохи фильмы снимали на киноплёнку. И в кинокамерах, и в кинопроекторах были грейферные механизмы, обеспечивавшие скачкообразное движение плёнки вдоль объектива (стандартно — 18 скачков в секунду). Движение этих механизмов задавал треугольник Рёло.

Третий пример — из области автомобилестроения. В конце 1940-х годов Ф. Г. Ванкель придумал схему двигателя без коленчатого вала, в котором поступательное движение поршней преобразуется во вращение вала мотора. В этом двигателе, называемом роторным, нет цилиндров. Ротор при вращении постоянно касается стенок камеры двигателя, разделяя рабочее пространство на три части. В двигателе Ванкеля форма ротора в сечении — треугольник Рёло.

Возвращаясь к геометрии, заметим, что если центр треугольника Рёло двигается по определённой замкнутой кривой, а сам треугольник при этом вращается вокруг центра, то он захватывает область, имеющую форму квадрата, углы которого немного закруглены. С использованием этой идеи создано сверло, позволяющее получать почти квадратные отверстия.

По материалам книги «Математическая составляющая». — М.: Математические этюды, 2015.